“Ma trận là gì?” là một trong những câu hỏi mà thichchiase nhận được từ nhiều bạn đọc dạo gần đây. Đây là một trong những mảng kiến thức được đánh giá là khó trên thực tế hiện nay. Đặc biệt trong lĩnh vực toán học. Vì vậy, tại bài viết hôm nay, hãy cùng thichchiase tìm hiểu về chủ đề ma trận trong toán học, cũng như vai trò của thuật ngữ này dưới phạm vi của những con số là gì nhé. Theo dõi ngay để nắm bắt cho mình những kiến thức hữu ích.
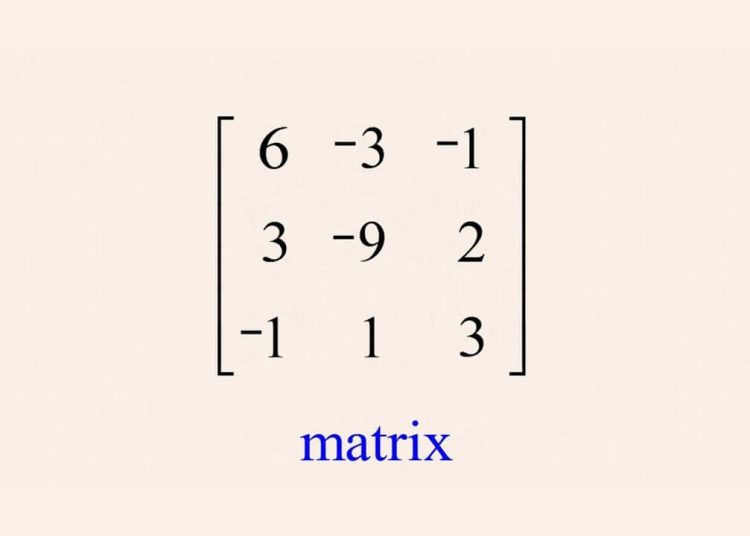
Ma trận là gì?
Là một khái niệm quan trọng trong toán học. Đặc biệt là trong các lĩnh vực như đại số tuyến tính, lý thuyết hệ thống, khoa học máy tính, và kỹ thuật. Vào thế kỷ 19, ma trận được giới thiệu bởi các nhà toán học hàng đầu trên thế giới. Ma trận đã trở thành một công cụ cơ bản và mạnh mẽ để giải quyết nhiều vấn đề phức tạp trong toán học và khoa học.
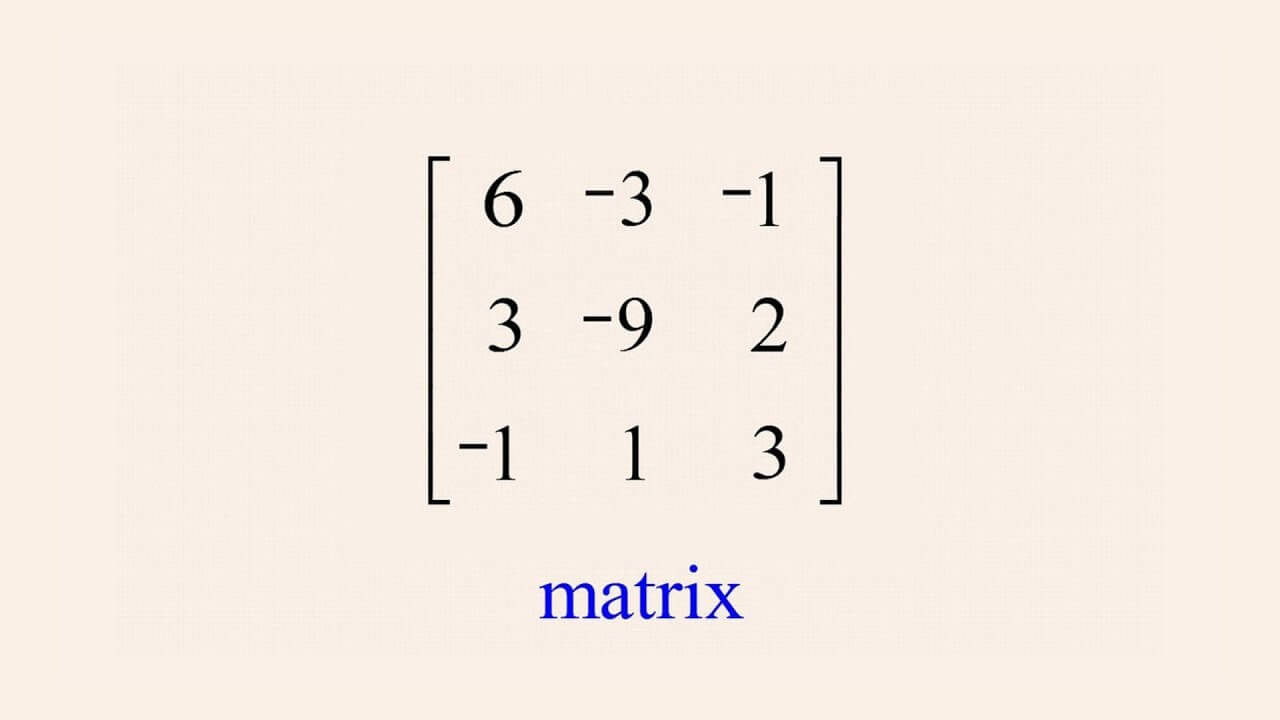
Ma trận được định nghĩa là một mảng chữ nhật gồm các số hoặc các đối tượng toán học khác. Được sắp xếp thành các hàng và các cột. Cách ký hiệu một ma trận thường là dùng chữ cái in hoa. Chẳng hạn như A,B,C. Một ma trận có m hàng và n cột được gọi là ma trận m x n. Mỗi phần tử trong ma trận được xác định bởi vị trí hàng và cột của nó và được ký hiệu là Aij.

Phân loại ma trận trong toán học
1. Ma Trận Vuông (Square Matrix)
- Là ma trận có số hàng bằng số cột (m = n).
- Ma trận vuông là cơ sở cho nhiều khái niệm và phương pháp trong đại số tuyến tính. Ví dụ như định thức, ma trận nghịch đảo và giá trị riêng.
2. Ma Trận Đơn Vị (Identity Matrix)
- Là ma trận vuông với các phần tử trên đường chéo chính đều bằng 1 và các phần tử khác đều bằng 0.
- Ma trận đơn vị đóng vai trò tương tự như số 1 trong phép nhân số học. Nó là ma trận trung tính trong phép nhân ma trận.
3. Ma Trận Đường Chéo (Diagonal Matrix)
- Là ma trận vuông mà các phần tử ngoài đường chéo chính đều bằng 0.
- Ma trận đường chéo thường dễ xử lý hơn trong các phép tính, và chúng thường xuất hiện trong việc chéo hóa ma trận.
4. Ma Trận Tam Giác (Triangular Matrix)
- Gồm hai loại chính là ma trận tam giác trên và ma trận tam giác dưới., Với các phần tử trên hoặc dưới đường chéo chính đều bằng 0.
- Ma trận tam giác thường xuất hiện trong giải pháp của hệ phương trình tuyến tính thông qua phương pháp khử.
5. Ma Trận Đối Xứng (Symmetric Matrix)
- Là ma trận vuông mà Aij= Aij cho mọi i và j.
- Ma trận đối xứng có các tính chất đặc biệt và thường xuất hiện trong các bài toán liên quan đến giá trị riêng và vector riêng.
6. Ma Trận Phép Chiếu (Projection Matrix)
- Là ma trận mà khi nhân với chính nó cho ra kết quả bằng chính nó ( P2=P)
- Ma trận phép chiếu được sử dụng trong nhiều ứng dụng. Bao gồm việc tìm các thành phần chính trong phân tích dữ liệu.

Ma trận giữ vai trò quan trọng trong toán học
- Giải hệ phương trình tuyến tính
Ma trận là công cụ chính để biểu diễn và giải hệ phương trình tuyến tính. Phương pháp ma trận như khử giúp tìm nghiệm của các hệ phương trình này một cách hiệu quả.
- Biến đổi tuyến tính
Trong đại số tuyến tính, ma trận đại diện cho các biến đổi tuyến tính. Chúng mô tả cách mà các vector trong không gian được dịch chuyển, xoay, co giãn, hoặc phản chiếu.
- Giá trị riêng và vector riêng
Các ma trận được sử dụng để tìm giá trị riêng và vector riêng. Là các khái niệm quan trọng trong nhiều lĩnh vực như cơ học lượng tử, ổn định hệ thống, và phân tích dữ liệu.
- Định thức và nghịch đảo ma trận
Định thức của một ma trận vuông cung cấp thông tin quan trọng về các tính chất của ma trận, bao gồm khả năng nghịch đảo của nó. Ma trận nghịch đảo là công cụ cần thiết trong việc giải các hệ phương trình tuyến tính và trong nhiều ứng dụng toán học khác.
- Phân tích dữ liệu
Trong phân tích dữ liệu và học máy, ma trận được sử dụng để biểu diễn dữ liệu, thực hiện các phép phân tích chính yếu và trong các phương pháp giảm kích thước dữ liệu.
- Lý thuyết đồ thị
Ma trận liên kết và ma trận trọng số là các công cụ quan trọng trong lý thuyết đồ thị, giúp biểu diễn các đồ thị và tính toán các tính chất của chúng như đường đi ngắn nhất, luồng cực đại, và nhiều bài toán khác.
Tổng kết
Ma trận là một phần không thể thiếu của toán học hiện đại. Nó còn được ứng dụng rộng rãi từ lý thuyết cơ bản đến các lĩnh vực khoa học và kỹ thuật. Sự hiểu biết về các loại ma trận và vai trò của chúng sẽ giúp chúng ta khai thác tối đa tiềm năng của công cụ mạnh mẽ này trong việc giải quyết các vấn đề phức tạp. Vậy là thichchiase vừa tổng hợp giúp bạn những thông tin quan trọng của ma trận trong toán học. Hy vọng bạn đã có thể nắm rõ kiến thức liên quan đến chủ đề “ma trận là gì?”. Cảm ơn bạn đã dành thời gian theo dõi bài viết của chúng tôi. Hẹn gặp lại bạn vào một ngày gần nhất tại website thichchiase.net.